Election Algorithm| Election Algorithm in Distributed System

Introduction:

The election algorithm in distributed systems is a mechanism used to select a coordinator or a leader among a group of process (nodes) . It’s particularly important in distributed systems where multiple nodes need to coordinate their activities, such as in distributed databases, cluster computing, or networked systems. Election algorithms are designed to choose a coordinator. It is a special purpose algorithm, which is run for selecting the coordinator process among N number of processes.

Election algorithm chooses a process from a group of processes to act as a coordinator. If the coordinator process crashes due to some reasons, then a new coordinator is elected from other processes. In general, election algorithms try to locate the process with the highest process number and designate it as coordinator. Every process knows the process number of every other process. One commonly used algorithm is the Bully Algorithm.

Requirement of Election Algorithm:

Many distributed algorithms require one process to act as coordinator, initiator, or otherwise perform some special role. The coordinator process plays an important role in the distributed system to maintain the consistency through synchronization.

Synchronization between processes often requires that one process acts as a coordinator. In those cases where the coordinator is not fixed, it is necessary that processes in a distributed computation decide on who is going to be that coordinator. Such a decision is taken by means of Election Algorithms. Election algorithms are primarily used in cases where the coordinator can crash. However, they can also be applied for the selection of superpeers in peer-to-peer systems.

Election algorithms are meant for electing a coordinator process from among the currently running processes in such a manner that at any instance of time there is a single coordinator for all processes in that system.

Election algorithm assumes that every active process in the system has a unique process number. The process with highest process number will be chosen as a new coordinator. Hence, when a coordinator fails, this algorithm elects that active process which has highest process number.

The goal of election algorithm is to choose and declare one and only process as the coordinator even if all processes participate in the election. And at the end of the election, all the processes should agree upon the new coordinator process without any confusion. Overall, the election algorithm plays a critical role in ensuring the reliability, scalability, and fault tolerance of distributed systems by facilitating the dynamic selection of leaders in a decentralized manner.

The need for an election algorithm in distributed systems arises from several key requirements and challenges inherent in such systems:

Fault Tolerance: Distributed systems often consist of multiple nodes that can fail independently due to hardware failures, software errors, or network partitions. To maintain system functionality in the presence of failures, it’s crucial to have a mechanism for dynamically electing new leaders or coordinators to take over the responsibilities of failed nodes.

Coordination: Many distributed systems require a single node to act as a coordinator or leader to coordinate the activities of other nodes, such as in distributed databases, consensus protocols, or cluster computing. An election algorithm ensures that a new coordinator can be quickly and efficiently elected when needed.

Scalability: As distributed systems grow in size, the overhead of centralized coordination or manual intervention becomes prohibitive. An election algorithm enables the automatic selection of leaders without requiring explicit configuration or management, thus supporting scalability.

Dynamic Membership: Distributed systems often have dynamic membership, where nodes can join or leave the system at any time. An election algorithm allows the system to adapt to changes in membership by electing new leaders as needed, ensuring continuity of operations.

Bully Algorithm:

Bully Algorithm is a type of Election Algorithm. The Bully Algorithm is one of the most well-known election algorithms used in distributed systems. This algorithm was proposed by Garcia-Molina (1982). The idea behind the Bully Algorithm is to elect the highest-numbered process (nodes) as the coordinator. This algorithm ensures that the node with the highest identifier becomes the coordinator in case of a failure or unavailability of the current coordinator. It allows nodes in a distributed system to elect a coordinator or leader among themselves when the current coordinator fails or becomes unreachable.

Here’s a simplified explanation of how Bully Algorithm works:

Initialization: Each node in the system has a unique identifier. Initially, all nodes are in a passive state.
Election Request: If a node detects that the coordinator has failed or become unreachable (e.g., due to a failure or timeout), it initiates an election by sending an election message to all nodes with higher identifiers.
Election Process: Upon receiving an election message, a node checks if its identifier is higher than the sender’s. If so, it responds with an “OK” message and starts its own election by sending an election message to all nodes with higher identifiers than itself. If not, it ignores the message.
Coordinator Election: Eventually, the election message reaches a node with the highest identifier (the “bully”) that doesn’t receive an “OK” message from any other node. This node becomes the new coordinator.
Coordinator Announcement: The new coordinator sends out a coordinator message to inform all other nodes about its status.
Reorganization: Nodes that receive the coordinator message update their local state to recognize the new coordinator and resume normal operations.

When any process notices that the coordinator is not active, crashed or no longer responding to requests, it initiates an election. A process, P, holds an election as follows:

1. P sends an ELECTION message to all processes with higher numbers.

2. If no one responds, P wins the election and becomes coordinator.

3. If one of the higher-ups answers, it takes over. P’s job is done or finish.

At any moment, a process can receive an ELECTION message from any one of its lower-numbered process. When such a message arrives, the receiver sends an OK message back to the sender to indicate that it is active and will take over. The receiver then holds an election, unless it is already holding one. Eventually, all processes give up but one, and that one is the new coordinator. It announces its victory by sending all processes a message telling them that starting immediately it is the new coordinator.If a process that was previously down comes back up, it holds an election. If it happens to be the highest-numbered process currently running, it will win the election and take over the coordinator’s job. Thus the biggest guy in town always wins, hence the name “Bully Algorithm.”

Figures below shows how the Bully Algorithm works:

Fig-1

The group consists of 8 processes, numbered from 0 to 7. Previously process 7 was the coordinator, but it has just crashed. Process 4 is the first one to notice this, so it sends ELECTION messages to all the processes higher than it, namely 5, 6, and 7 as shown in Fig-1.

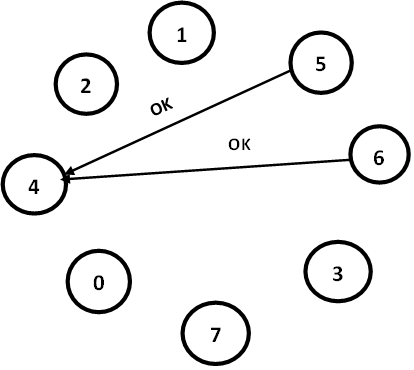
Fig-2

Processes 5 and 6 both respond with OK, as shown in Fig-2. Upon getting the responses, process 4 job is over. It knows that one of these will take over and become coordinator. It just sits back and waits to see who the winner will be.

In Fig-3, both 5 and 6 hold elections, each one sending ELECTION messages to those processes higher than itself.

Fig-3

In Fig-4 process 6 tells 5 that it will take over with an OK message. At this point 6 knows that 7 is dead and that it (6) is the winner.

Fig-4

If there is state information to be collected from disk or elsewhere to pick up where the old coordinator left off, 6 must now do what is needed. When it is ready to take over, 6 announces this by sending a COORDINATOR message to all running processes shown in fig-5.

Fig-5

When 4 gets this message, it can now continue with the operation it was trying to do when it discovered that 7 was dead, but using 6 as the coordinator this time. In this way the failure of 7 is handled and the work can continue.

If process 7 is ever restarted, it will just send all the others a COORDINATOR message and bully them into submission.

There are three types of messages that processes will exchange between each other during the Bully Algorithm:

1. ELECTION message

2. OK message

3. Coordinator message

An ELECTION message is sent to announce an election, an OK message is sent in response to an ELECTION message and a COORDINATOR message is sent to announce the identity of the elected process – the new ‘coordinator’.

Ring Algorithm:

The Ring Algorithm is a common election algorithm used in distributed systems. This algorithm is suitable for a collection of processes arranged in a logical ring. The Ring Election Algorithm is based on the ring topology with the process ordered logically and each process knows its successor in an unidirectional way, either clockwise or anticlockwise.

The Ring Algorithm ensures that the node with the highest identifier becomes the coordinator without the need for central coordination or global knowledge of the system state. It’s particularly suitable for systems where nodes are organized in a ring-like structure, such as in some peer-to-peer networks or distributed sensor networks.

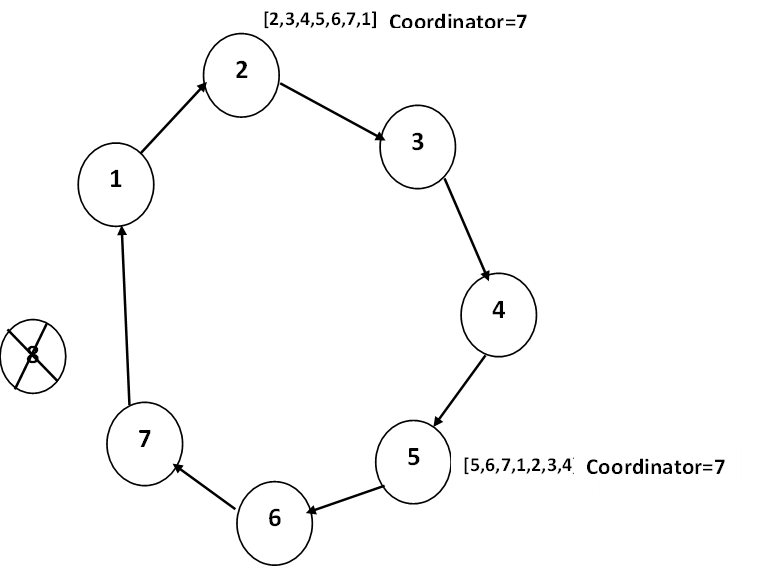
When any process notices that the coordinator process has crashed, it creates an ELECTION message, containing its own process number and sends the message to its successor. If the successor is down, the message would skip the successor and goes to the next process after its successor. On receiving an ELECTION message, a process adds its process number to the message before forwarding it to the next process in the ring.

Finally, the ELECTION message comes back to the process which initiated the message. Election initiator process analyses and finds the highest process number ( coordinator) among the available processes converts the ELECTION message into COORDINATOR message and removes all the process number from the list except the highest process number. This COORDINATOR message is circulated along the ring for one circulation to inform the running processes about who the new coordinator is. When this message is circulated once, it is discarded and the Election Algorithm ends here.

Working of Ring Algorithm explained below with an example:

In this example, Initially there are 8 process and all the processes are arranged in a logical ring. Previously process 8 was the coordinator, but it has crashed. Process 2 and 5 discover simultaneously that the previous coordinator, process 8 has crashed. Each of these builds an ELECTION message and each of them starts circulating its message, independent of the other one.

Process 2 initiates an election…